【睿尔曼-RealMan】手眼标定理论
Jehan 2024-03-14
1.相机成像模型

1.1小孔成像和四个坐标系
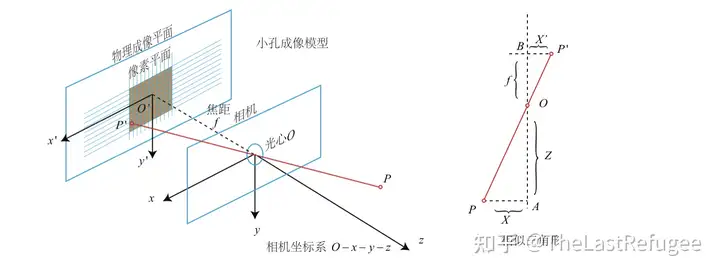
1.1.1 小孔成像
1.1.2 世界坐标系
物体所在的坐标系,世界坐标系的原点和坐标轴可以是任意位置,任意方向的。
1.1.3 相机坐标系
设O-x-y-z为相机坐标系,习惯把z轴指向相机前方,x向右,y向下。O为摄像机的光心

1.1.4 像平面坐标系
经过小孔成像后得到的二维坐标系,以图像的中心为圆点,单位mm
1.1.5 像素坐标系
原点o'位于图像的左上角,u轴向右与x轴平行,v轴向下与y轴平行,单位是像素。
1.2 四个坐标系之间的关系
1.2.1 世界坐标系与相机坐标系
物体还是那个物体,在世界坐标系和相机坐标系的位姿不同。

1.2.2 相机坐标系和像平面坐标系

设O-x-y-z为相机坐标系,习惯上我们把z轴指向相机前方,x向右,y向下。O为摄像机的光心,也是针孔模型中的针孔。
设真实世界点中的P在相机坐标系的坐标为

,成像的点P'的坐标为

, 物理成像平面和光心的距离为f(即为焦距)。
根据右图中的三角形相似关系,有:

其中,有负号是因为坐标轴方向,也就表示了成的像是倒立的。
忽略方向,对称后的关系:

整理解出P'的坐标:

同样可以用矩阵表示:

上面式子就描述了P点与它所成像的坐标关系
1.2.3 像平面坐标系和像素坐标系

像素坐标系的定义是:原点0'位于图像左上角,u轴向右与x轴平行,v轴向下与y轴平行。
成像是在以Oimg为坐标系原点的像平面坐标系中,但是做图像存储的时候是从左上角开始存储的(像素坐标系),方便数据的读写,所以像平面坐标系的一个坐标转化到像素坐标系需要做一个平移。x,y方向的平移距离是Cx和Cy,单位是像素。
因为像平面坐标系的单位是mm,像素坐标系的单位是像素,所以还需要进行缩放,在u轴和v轴上的缩放系数分别是

它们的单位是 像素/毫米 。

矩阵形式:
1.2.4 完整坐标系转换
从世界坐标系到像素坐标系,写成矩阵形式,可以得到:

M1为相机内参,包括经过缩放的焦距,光轴与图像平面的焦点位置等参数,表示为:

M2为相机外参,是世界坐标系到相机坐标系的转换关系,是世界坐标系到相机坐标系的位姿矩阵
1.3 实战
1.3.1 采图
1.3.2 opencv运算
def func():
path = os.path.dirname(__file__)
# 角点的个数以及棋盘格间距
XX = 11 #标定板的中长度对应的角点的个数
YY = 8 #标定板的中宽度对应的角点的个数
L = 0.03 #标定板一格的长度 单位为米
# 设置寻找亚像素角点的参数,采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 获取标定板角点的位置
objp = np.zeros((XX * YY, 3), np.float32)
objp[:, :2] = np.mgrid[0:XX, 0:YY].T.reshape(-1, 2) # 将世界坐标系建在标定板上,所有点的Z坐标全部为0,所以只需要赋值x和y
objp = L*objp
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
for i in range(0, 50): #标定好的图片在iamges_path路径下,从0.jpg到x.jpg 一次采集的图片最多不超过50张,我们遍历从0.jpg到50.jpg ,选择能够读取的到的图片
image = f"{iamges_path}\\{i}.jpg"
if os.path.exists(image):
img = cv2.imread(image)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
size = gray.shape[::-1]
ret, corners = cv2.findChessboardCorners(gray, (XX, YY), None)
if ret:
obj_points.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria) # 在原角点的基础上寻找亚像素角点
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)
N = len(img_points)
# 标定,得到图案在相机坐标系下的位姿
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
cv2.calibrateCamera函数通过 输入 标定板对应的 世界坐标系下的3D坐标,和提取的角点的像素坐标系下的像素坐标,求解相机的内参数和每一个视角的外参数。
2.手眼标定
2.1眼在手外
眼在手外固定关系是标定板与机械臂末端的关系固定,以及相机与机器人基座标的关系固定
求解目标:相机到机械臂基座坐标系的变换矩阵

实现方法:1.把标定板固定在机械臂末端
2.移动机械臂末端,使用相机拍摄不同机械臂姿态下的标定板图片n张 (10~20)
已经对每张图片:

其中:

因为标定板固定在机械臂末端上,标定板到机械臂末端的变化矩阵不变
则可以得到如下等式:

2.2 眼在手上
对于眼在手上的标定,标定等式(AX = XB)建立在两个不变量的基础上,分别是标定板与机械臂基坐标的关系不变,以及相机与机械臂末端的关系不变
求解目标:相机到机械臂末端坐标系的变换矩阵

实现方法:1.把标定板放到固定位置不动
2.移动机械臂末端,从不同角度拍摄n张标定板照片。(10~20)
已经对每张图片:

其中:
 2.3 解方程 AX = XB
2.3 解方程 AX = XB
眼在手外:

眼在手上:

无论是眼在手外还是眼在手内,我们都可以得到一个经典的方程组AX = XB,这个方程组里有n-1个方程,(n是拍摄的图片数量)
其中X即为我们需要求得的转换矩阵,里面有旋转矩阵和平移向量。
2.4 注意
眼在手外和眼在手上都有两个不变的关系:
眼在手上:
•相机和机械臂末端
•标定板和机械臂基座
我们需要求的是相机和机械臂末端之间关系,用另一个不变的关系标定板和机械臂基座构建等式

眼在手外:
•标定板和机械臂末端
•相机和机械臂基座
我们需要求的是相机和机械臂基座之间关系,用另一个不变的关系标定板和机械臂末端构建等式

2.5 运用

0 条评论








撰写评论