一、基本步骤

(1)在机器人动作范围内找一个非常精确的固定点作为参考点；

(2)在工具上确定一个参考点（最好是工具中心点Tool Center Point, TCP）;

(3)手动操纵机器人的方法移动TCP，以四种不同的工具姿态与固定点刚好碰上。

(4)前三个点任意姿态，第四点是用工具的参考点垂直于固定点，第五点是工具参考点从固定点向将要设定的TCP的x方向移动，第六点是工具参考点从固定点向将要设定的TCP的在z方向移动。如下图所示。

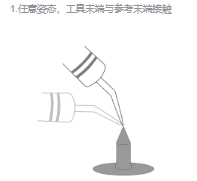
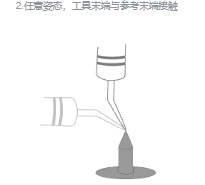
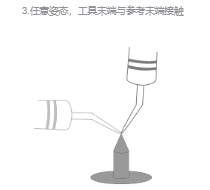
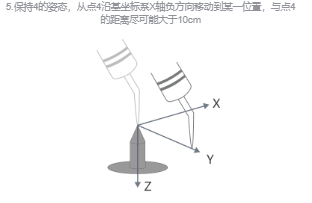
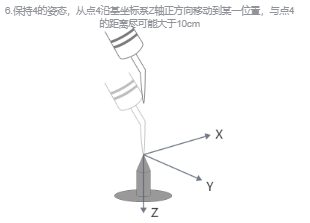
（5）通过前4个点的位置数据即可计算出TCP的位置，通过后2个点即可确定TCP的姿态。

二、标定过程

1、TCP位置标定

假设取1、2、3、4四个标定点之间相差90°且不在同一平面上，如下图所示：

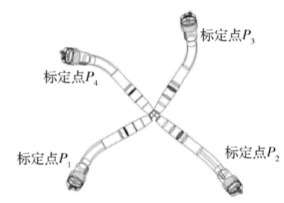
给定如下坐标定义：

基坐标系：B 末端坐标系：E 工具坐标系：T

给定如下变换矩阵定义：

末端坐标系 E 相对于基坐标系 B的变换关系: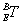

工具坐标系T 相对于末端坐标系 E的变换关系:

工具坐标系T 相对于基坐标系 B的变换关系: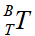

可知:

 对于选定位置点i = 1、2、3、4，有：

(1)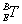不等，设：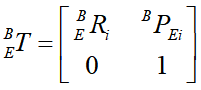

(2)不等，但其位置相等，设：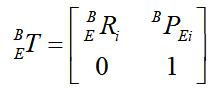

(3)不等，但其位置相等，设:

所以有：

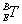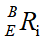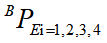在实际中,由机器人正解方程可以直接测得，因此，我们直接读取四个位置点的姿态和位置，假设：

两式相减可得：

同理可得：

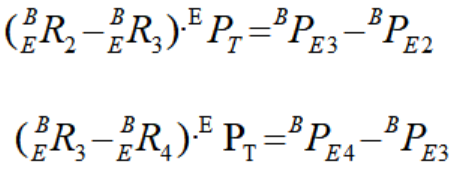
由上式可得：

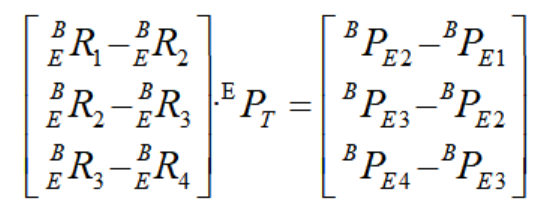
为 3x1 列向量，而等式右边为 9x3的矩阵，因此上式方程为不相容方程组，不可直接用非齐次线性方程组求解的方法或者solve求解。采用最小二乘法的矩阵形式，因其系数矩阵不是方阵，不可直接求逆， 因此使用广义逆。采用高斯消元法得到：

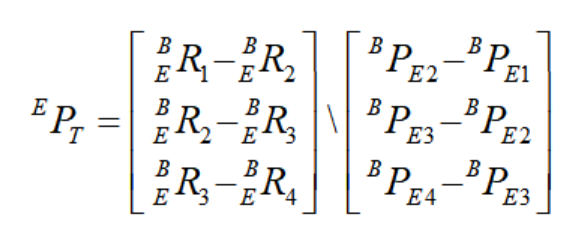
则上式所求得的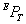即为TCP的位置向量。

2、TCF姿态标定

前面已经得到工具坐标系(TCF)的位置，而计算TCP姿态采用z/x方向标定。此过程中TCF的姿态保持不变，取第一个姿态标定点为位置点4；机器人从位置点4出发，沿-x方向移动一定距离得到位置点5；机器人从位置点4出发，沿+z方向移动一定距离得到位置点6。

由于3个标定点中的TCF姿态不变，所以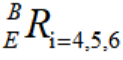均相等，保持不变，故可得到工具坐标系 T 的 x 轴轴向向量X，且:

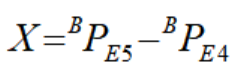
同理，可得到工具坐标系 T 的 z 轴轴向向量Z，且：

进而由右手定则得工具坐标系 T 的 y 轴轴向向量 Y:

为进一步保证坐标系矢量的正交性，重新计算Z ：

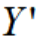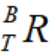将X,Y,Z进行单位化得到,，,得到工具坐标 T 相对于基坐标 B 的姿态，且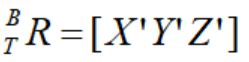，又末端坐标系 E 旋转矩阵为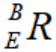,且：

可得到工具坐标系的旋转矩阵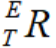，即：

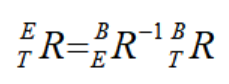
3、标定结果

得到工具坐标系,标定为：

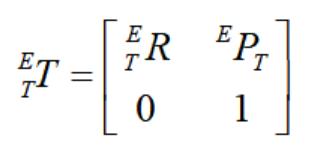
显然，TCF六点法标定的最小条件是能够获取到6个位置点的位姿，且为使式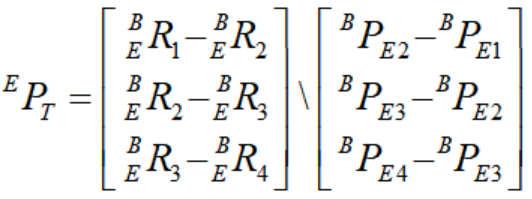有解，应保证位置点1，2，3，4不在同一平面上。